We often need to know the velocity of a particle at a given moment, rather than the average velocity over a finite time interval. For example, even if you want to calculate your average velocity during a long car trip, you would especially like to know your velocity when you notice the police car parked along the road in front of you. In other words, you would like to be able to specify your velocity as accurately as you can specify your position by noting what happens at a specific clock reading, that is, at a given time. It may not be immediately obvious how to do this. What does it mean to talk about the velocity at which something moves if we "freeze time" and speak only of an individual moment? It is a subtle point that was not completely understood until the end of the 17th century. At that time, with the invention of computation, scientists began to understand how to describe the motion of an object at any time.
To see how this is done, consider Figure 2.3a, which is a reproduction of the graph in Figure 2.1b. We have already discussed the average velocity for the interval in which the car passed from position A to position B (given by the slope of the dark blue line) and for the interval during which it was moved from A to F. In your opinion, which of these two lines is an approximation closer to the initial velocityof the car? The car starts to move to the right, which we have defined as the positive direction. Therefore, being positive, the value of the average velocity during the interval A to B is more representative of the initial value than is the value of the average velocity during the interval A to F. now at the dark blue line and slide point B to the left along the curve towards point A, as shown in Figure 2.3b. The line between the points becomes steeper and, as the two points become extremely close to each other, the line becomes a line tangent to the curve, indicated by the green line in Figure 2.3b. The slope of this tangent line represents the velocity of the car when we started taking data, to the point A. What we did is determine the instantaneous velocity at that moment. In other words, the instantaneous velocity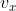 
is equal to the limit value of the ratio 
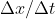when 
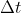approaches zero:
In computation notation, this limit is called the derivative of x with respect to t, written :
The instantaneous velocity can be positive, negative or zero. When the slope of the position-time graph is positive, for example at any time during the first 10 seconds of Figure 2.3, 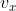is positive: the car moves to larger values of x. After point ", 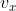is negative because the slope is negative, the car is closer to the lower values of x point", the slope and the instantaneous velocity are zero - the car is momentarily at rest.
From there, we use the word velocity to designate instant velocity. When one is interested in the average velocity, one will always use the average adjective.
The instantaneous velocity of a particle is defined as the magnitude of its instantaneous velocity. As with the average velocity, the instantaneous velocity has no associated direction and therefore bears no algebraic sign. For example, if a particle has an instantaneous velocity of +25 m / s along a given line and another particle has an instantaneous velocity of - 25 m / s along the same line, both have a velocity of 25 m/s.
