Science and engineering are based on measurements and comparisons. Thus, we need rules about how things are measured and compared, and we need experiments to establish the units for those measurements and comparisons. One purpose of physics (and engineering) is to design and conduct those experiments. For example, physicists strive to develop clocks of extreme accuracy so that any time or time interval can be precisely determined and compared. You may wonder whether such accuracy is actually needed or worth the effort. Here is one example of the worth: Without clocks of extreme accuracy, the Global Positioning System (GPS) that is now vital to worldwide navigation would be useless.
1.2. Measuring Things
We discover physics by learning how to measure the quantities involved in physics. Among these quantities are length, time, mass, temperature, pressure, and electric current. We measure each physical quantity in its own units, by comparison with a standard. The unit is a unique name we assign to measures of that quantity for example, meter (m) for the quantity length. The standard corresponds to exactly 1.0 unit of the quantity. As you will see, the standard for length, which corresponds to exactly 1.0 m, is the distance traveled by light in a vacuum during a certain fraction of a second. We can define a unit and its standard in any way we care to. However, the important thing is to do so in such a way that scientists around the world will agree that our definitions are both sensible and practical.
Once we have set up a standard—say, for length—we must work out procedures by which any length whatever, be it the radius of a hydrogen atom, the wheelbase of a skateboard, or the distance to a star, can be expressed in terms of the standard. Rulers, which approximate our length standard, give us one such procedure for measuring length. However, many of our comparisons must be indirect. You cannot use a ruler, for example, to measure the radius of an atom or the distance to a star.
There are so many physical quantities that it is a problem to organize them. Fortunately, they are not all independent; for example, speed is the ratio of a length to a time. Thus, what we do is pick out by international agreement a small number of physical quantities, such as length and time, and assign standards to them alone. We then define all other physical quantities in terms of these base quantities and their standards (called base standards). Speed, for example, is defined in terms of the base quantities length and time and their base standards.
Base standards must be both accessible and invariable. If we define the length standard as the distance between one’s nose and the index finger on an outstretched arm, we certainly have an accessible standard—but it will, of course, vary from person to person. The demand for precision in science and engineering pushes us to aim first for invariability. We then exert great effort to make duplicates of the base standards that are accessible to those who need them.
1.3. Standarts of Length, Mass, and Time
The laws of physics are expressed as mathematical relationships among physical quantities that we will introduce and discuss throughout the book. Most of these quantities are derived quantities, in that they can be expressed as combinations of a small number of basic quantities. In mechanics, the three basic quantities are length, mass, and time. All other quantities in mechanics can be expressed in terms of these three.
If we are to report the results of a measurement to someone who wishes to reproduce this measurement, a standard must be defined. It would be meaningless if a visitor from another planet were to talk to us about a length of 8 “glitches” if we do not know the meaning of the unit glitch. On the other hand, if someone familiar with our system of measurement reports that a wall is 2 meters high and our unit of length is defined to be 1 meter, we know that the height of the wall is twice our basic length unit. Likewise, if we are told that a person has a mass of 75 kilograms and our unit of mass is defined to be 1 kilogram, then that person is 75 times as massive as our basic unit.1 Whatever is chosen as a standard must be readily accessible and possess some property that can be measured reliably. Measurements taken by different people in different places must yield the same result.
In 1960, an international committee established a set of standards for the fundamental quantities of science. It is called the SI (Système International), and its units of length, mass, and time are the meter, kilogram, and second, respectively. Other SI standards established by the committee are those for temperature (the kelvin), electric current (the ampere), luminous intensity (the candela), and the amount of substance (the mole).
Length
In A.D. 1120 the king of England decreed that the standard of length in his country would be named the yard and would be precisely equal to the distance from the tip of his nose to the end of his outstretched arm. Similarly, the original standard for the foot adopted by the French was the length of the royal foot of King Louis XIV. This standard prevailed until 1799, when the legal standard of length in France became the meter, defined as one ten-millionth the distance from the equator to the North Pole along one particular longitudinal line that passes through Paris.
Many other systems for measuring length have been developed over the years, but the advantages of the French system have caused it to prevail in almost all countries and in scientific circles everywhere. As recently as 1960, the length of the meter was defined as the distance between two lines on a specific platinum–iridium bar stored under controlled conditions in France. This standard was abandoned for several reasons, a principal one being that the limited accuracy with which the separation between the lines on the bar can be determined does not meet the current requirements of science and technology. In the 1960s and 1970s, the meter was defined as 1 650 763.73 wavelengths of orange-red light emitted from a krypton-86 lamp. However, in October 1983, the meter (m) was redefined as the distance traveled by light in vacuum during a time of 1/299 792 458 second. In effect, this latest definition establishes that the speed of light in vacuum is precisely 299 792 458 meters per second.
Table 1.1 lists approximate values of some measured lengths. You should study this table as well as the next two tables and begin to generate an intuition for what is meant by a length of 20 centimeters, for example, or a mass of 100 kilograms or a time interval of 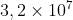 seconds.
seconds.
Mass
The SI unit of mass, the kilogram (kg), is defined as the mass of a specific platinum–iridium alloy cylinder kept at the International Bureau of Weights and Measures at Sèvres, France. This mass standard was established in 1887 and has not been changed since that time because platinum–iridium is an unusually stable alloy. A duplicate of the Sèvres cylinder is kept at the National Institute of Standards and Technology (NIST) in Gaithersburg, Maryland (Fig. 1.). Table 1.2 lists approximate values of the masses of various objects
Figure 1. (a) The National Standard Kilogram No. 20, an accurate copy of the International Standard Kilogram kept at Sèvres, France, is housed under a double bell jar in a vault at the National Institute of Standards and Technology. (b) The nation’s primary time standard is a cesium fountain atomic clock developed at the National Institute of Standards and Technology laboratories in Boulder, Colorado. The clock will neither gain nor lose a second in 20 million years
Time
Before 1960, the standard of time was defined in terms of the mean solar day for the year 1900. (A solar day is the time interval between successive appearances of the Sun at the highest point it reaches in the sky each day.) The second was defined as (1/60)(1/60)(1/24) of a mean solar day. The rotation of the Earth is now known to vary slightly with time, however, and therefore this motion is not a good one to use for defining a time standard. In 1967, the second was redefined to take advantage of the high precision attainable in a device known as an atomic clock (Fig. 1.1b), which uses the characteristic frequency of the cesium-133 atom as the “reference clock.” The second (s) is now defined as 9 192 631 770 times the period of vibration of radiation from the cesium atom.
To keep these atomic clocks and therefore all common clocks and watches that are set to them synchronized, it has sometimes been necessary to add leap seconds to our clocks. Since Einstein’s discovery of the linkage between space and time, precise measurement of time intervals requires that we know both the state of motion of the clock used to measure the interval and, in some cases, the location of the clock as well. Otherwise, for example, global positioning system satellites might be unable to pinpoint your location with sufficient accuracy, should you need to be rescued.
Approximate values of time intervals are presented in Table 1.3.
In addition to SI, another system of units, the U.S. customary system, is still used in the United States despite acceptance of SI by the rest of the world. In this system, the units of length, mass, and time are the foot (ft), slug, and second, respectively. In this text we shall use SI units because they are almost universally accepted in science and industry. We shall make some limited use of U.S. customary units in the study of classical mechanics.
In addition to the basic SI units of meter, kilogram, and second, we can also use other units, such as millimeters and nanoseconds, where the prefixes milli- and nanodenote multipliers of the basic units based on various powers of ten. Prefixes for the various powers of ten and their abbreviations are listed in Table 1.4. For example, 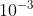 m is equivalent to 1 millimeter (mm), and
m is equivalent to 1 millimeter (mm), and 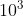 m corresponds to 1 kilometer (km). Likewise, 1 kilogram (kg) is
m corresponds to 1 kilometer (km). Likewise, 1 kilogram (kg) is 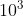 grams (g), and 1 megavolt (MV) is
grams (g), and 1 megavolt (MV) is 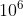 volts (V).
volts (V).
References:
Halliday D, Resnick R, Walker J, 2011. Fundamental of Physics 9th Edition. ISBN: 978-0-470-56473-8. John Wiley & Sons, Inc.
Serway R.A and Jewett J.W. 2004. Physics For Scientists and Engineers 6th Edition. ISBN: 0534408427. Thomson Brooks/Cole.





